A honeycomb is a very stable structure. If it has a larger hole, however, stability is largely lost. What might a honeycomb look like, which survives external forces in spite of a hole? Such stable types of known constructions might be useful in architecture or when developing new construction materials. So far, the mathematical expenditure required has been very high and did not lead to the success desired in mechanics. Researchers of Karlsruhe Institute of Technology (KIT) have now found a new principle that considerably facilitates the mathematical approach and produces promising results with simple means.
The conception of “coordinate transformation” may sound complex, but such mathematical transformations are rather helpful: A mesh of connected points is drawn onto a rubber skin. Coordinate transformation is simulated by extending and distorting this rubber surface. When the assumed mesh can be mapped onto material distribution, a rather universal design approach results. It can be used to direct e.g. mechanical forces acting on the material along the tracks desired.
For light, such transformations are based on the mathematics of transformation optics. So far, however, it has been impossible to transfer this principle to real materials and components in mechanics. The mathematics made impossible requirements on the material.
To overcome these difficulties, researchers of the KIT Institute of Applied Physics around first author Tiemo Bückmann found a new, simple method. “We imagined a network of electric resistors,” Bückmann explains. “The wire connections between the resistors may be chosen to be of variable length, but their value does not change. Electric conductivity of the network even remains unchanged, when it is deformed.”
The researchers transferred this thought experiment to practice. “In mechanics, this principle is found again when imagining small springs instead of resistors,” Tiemo Bückmann says. “We can make single springs longer or shorter when adapting their shapes, such that the forces between them remain the same. This simple principle saves computation expenditure and allows for the direct transformation of real materials.”
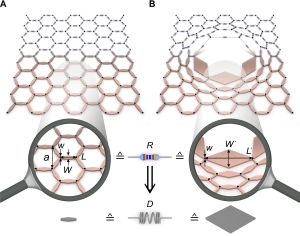
The researchers tested their method in a model experiment with a material made of printed polymer. A stable hexagonal honeycomb structure was provided with a hole. Due to its reduced stability, the distorting forces first caused an error of more than 700 percent. After application of the newly developed transformation, the error amounted to 26 percent only. The results have just been published in the proceedings of the National Academy of Sciences (PNAS).
Applications are manifold, as the new method can be used to calculate known composite materials or mechanical support constructions. Even special designs will react as stably as possible to external forces – as if the support construction would not have been deformed.

Analysis of a hole in a hexagonal structure: External forces strongly deform the structure, the structure is unstable. By means of the new construction method, this error can be reduced strongly. (Figure: T. Bückmann)
Being “The University in the Helmholtz Association”, KIT creates and imparts knowledge for the society and the environment. It is the objective to make significant contributions to the global challenges in the fields of energy, mobility, and information. For this, about 10,000 employees cooperate in a broad range of disciplines in natural sciences, engineering sciences, economics, and the humanities and social sciences. KIT prepares its 22,800 students for responsible tasks in society, industry, and science by offering research-based study programs. Innovation efforts at KIT build a bridge between important scientific findings and their application for the benefit of society, economic prosperity, and the preservation of our natural basis of life. KIT is one of the German universities of excellence.